Quando Planck era estudante, três grandes nomes dominavam o cenário da física alemã, Clausius, Helmholtz e Kirchhoff. Desses foi Clausius que mais o influenciou, pela "clareza e poder de persuasão da linguagem''.
Tomando como ideal de física a formulação que este deu da segunda lei da termodinâmica, jamais alterada desde 1865, Planck assim expressou seu ideal:O que me interessou desde sempre na física foram as grandes leis gerais, válidas para todo o conjunto de fenômenos, independentes das propriedades particulares dos corpos que participam do processo. Bem de acordo com este programa, Planck escolheu como tema de pesquisa a segunda lei da termodinâmica, que desejava demonstrar como lei exata, conseqüência das leis da mecânica.
Posteriormente, convencido da implausibilidade de obtenção por esse meio da lei que, como gostava de salientar, fornece a única origem para a "flexa do tempo'' (por causa do teorema dos ciclos de Poincaré), buscou a demonstração da segunda lei no eletromagnetismo, que passou então a estudar profundamente. Foi, assim, naturalmente levado ao problema de determinar a função universal de Kirchhoff: tratava-se de um resultado universal, bem a seu gosto, e envolvia, em toda a sua profundidade, o eletromagnetismo.
Tomando como ideal de física a formulação que este deu da segunda lei da termodinâmica, jamais alterada desde 1865, Planck assim expressou seu ideal:O que me interessou desde sempre na física foram as grandes leis gerais, válidas para todo o conjunto de fenômenos, independentes das propriedades particulares dos corpos que participam do processo. Bem de acordo com este programa, Planck escolheu como tema de pesquisa a segunda lei da termodinâmica, que desejava demonstrar como lei exata, conseqüência das leis da mecânica.
Posteriormente, convencido da implausibilidade de obtenção por esse meio da lei que, como gostava de salientar, fornece a única origem para a "flexa do tempo'' (por causa do teorema dos ciclos de Poincaré), buscou a demonstração da segunda lei no eletromagnetismo, que passou então a estudar profundamente. Foi, assim, naturalmente levado ao problema de determinar a função universal de Kirchhoff: tratava-se de um resultado universal, bem a seu gosto, e envolvia, em toda a sua profundidade, o eletromagnetismo.
Desde a descoberta de Kirchhoff vários resultados parciais importantes tinham sido obtidos, por alguns dos melhores físicos de então. Primeiro, Boltzmann obteve o resultado empírico de Stefan, de que a densidade de energia da radiação no equilíbrio dependia da temperatura na forma
| |
onde 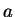 é uma constante. Para obter este resultado, Boltzmann usou a relação de Maxwell
é uma constante. Para obter este resultado, Boltzmann usou a relação de Maxwell 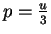 , que dá a pressão da radiação em termos da densidade de energia. Em um cilindro provido de um êmbolo existe radiação em equilíbrio à temperatura T. O volume do cilindro é
, que dá a pressão da radiação em termos da densidade de energia. Em um cilindro provido de um êmbolo existe radiação em equilíbrio à temperatura T. O volume do cilindro é 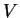 . A pressão da radiação faz com que o êmbolo se mova lentamente, realizando o trabalho
. A pressão da radiação faz com que o êmbolo se mova lentamente, realizando o trabalho 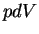 . A energia total da radiação sendo
. A energia total da radiação sendo 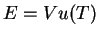 , temos
, temos
Êste trabalho foi considerado uma ``pérola''da termodinâmica, por sua simplicidade e audácia. De fato, a radiação é tratada como um gás, e uma entropia é associada a ela. Note-se ainda que a existência da pressão da radiação, e a veracidade da fórmula de Maxwell, só viriam a ser comprovadas experimentalmente em 1905, por Lebedev.
Em 1893 Willy Wien demonstrou o que seria o resultado mais forte possível de obter usando apenas as leis gerais da termodinâmica e do eletromagnetismo. Com grande virtuosismo no uso de espelhos móveis, Wien obteve a expressão
onde 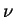 é, como sempre, a freqüência, e
é, como sempre, a freqüência, e 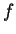 é uma função que não se pode determinar por este método. Assim, a busca da função universal ficara reduzida à procura de uma função de uma, que, aliás, apresenta um tratamento magnífico de todo o problema do corpo negro. variável. A demonstração mais simples da lei de Wien, baseada quase que só em análise dimensional, encontra-se no excelente texto de Sommerfeld, "Thermodynamics and Statistical Mechanics''
é uma função que não se pode determinar por este método. Assim, a busca da função universal ficara reduzida à procura de uma função de uma, que, aliás, apresenta um tratamento magnífico de todo o problema do corpo negro. variável. A demonstração mais simples da lei de Wien, baseada quase que só em análise dimensional, encontra-se no excelente texto de Sommerfeld, "Thermodynamics and Statistical Mechanics''
O próximo passo veio do próprio Wien, que propôs a seguinte fórmula empírica inspirada em seu resultado termodinâmico:
Esta fórmula obteve muito boa acolhida, estando em bom acordo com a experiência até meados de 1900. Nesta ocasião, então, Rubens conseguiu realizar medidas precisas para 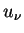 para grandes comprimentos de onda, que era o grande problema experimental.
para grandes comprimentos de onda, que era o grande problema experimental.
PARTE I
PARTE II
PARTE IV
Nenhum comentário:
Postar um comentário