Como mencionamos, Planck esperava poder deduzir a segunda lei da termodinâmica como lei exata, isto é, não estatística, valendo-se do eletromagnetismo. Para esse fim aprofundou-se nessa teoria, à qual chegou a dar contribuições importantes. Por exemplo, a famosa fórmula de Larmor,
que dá a potência irradiada por um oscilador de Hertz, foi obtida previamente por Planck.
Suponhamos um oscilador harmônico cuja massa possui também uma carga. Seja 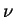 a freqúência natural do oscilador. Posto numa região onde existe radiação em equilíbrio térmico, o oscilador executará oscilações forçadas, sendo a ``driving force'' a força elétrica que atua sobre a carga. Planck mostrou que, no equilíbrio (a dissipação considerada é a reação da radiação) estabelece-se a seguinte relação:
a freqúência natural do oscilador. Posto numa região onde existe radiação em equilíbrio térmico, o oscilador executará oscilações forçadas, sendo a ``driving force'' a força elétrica que atua sobre a carga. Planck mostrou que, no equilíbrio (a dissipação considerada é a reação da radiação) estabelece-se a seguinte relação:
onde
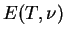
é a energia média por período do oscilador. Num certo sentido, Planck construiu um sintetizador da radiação térmica. Note ainda que a equação acima já tem a forma da lei de Wien, sendo que a procura da função crucial
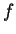
de Wien, pode ser agora feita trabalhando-se com os osciladores. Se, nesse instante, Planck, para o cálculo da energia média, tivesse usado a estatística clássica, teria posto
ou seja, teria obtido a lei de Rayleigh (também conhecida como Rayleigh-Jeans, por razões que me escapam) um ano antes de Lord Rayleigh. Para uma dedução completa destes resultados, veja a referência[
13].
Heinrich Rubens e Ferdinand Kurlbaum realizaram, em 1900, medidas na região do infra-vermelho (
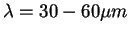
) e concluíram que a fórmula empírica de Wien não funcionava aí. Antes deles, mas com argumentos menos contundentes, Lummer e Pringsheim tinham chegado à mesma conclusão.
Em 7 de outubro, um domingo, Rubens e sua esposa visitaram os Plancks, e Rubens relatou que achara que 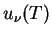 devia ser proporcional a
devia ser proporcional a 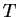 para
para 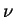 pequeno, o que era inconsistente com a fórmula de Wien. Logo que as visitas saíram, Planck atacou o problema de achar uma nova fórmula empírica que satisfizesse a nova exigência, e obteve, já numa notação que ele introduziria dois meses depois6
pequeno, o que era inconsistente com a fórmula de Wien. Logo que as visitas saíram, Planck atacou o problema de achar uma nova fórmula empírica que satisfizesse a nova exigência, e obteve, já numa notação que ele introduziria dois meses depois6
Esta fórmula teve um tal sucesso na descrição dos dados experimentais que Planck decidiu que tinha absolutamente de deduzi-la de primeiros princípios ``qualquer que seja o custo''.
Planck voltou então ao problema dos osciladores. Tudo estava em calcular a energia média, denotada acima por
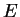
. Para osciladores em equilíbrio com radiação térmica à temperatura
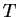
, temos
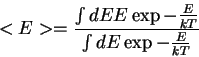
= \frac{\int dE E \exp{-\frac{E}{kT}}}{\int dE \exp{-\frac{E}{kT}}} \end{displaymath}" width="199" border="0" height="57">
que é a fórmula clássica de Boltzmann. Sem mais hipóteses sobre
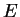
obtemos
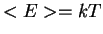
=kT$" width="103" align="middle" border="0" height="34">, e a fórmula (incorreta) de Rayleigh. De maneira inteiramente pragmática, para obter a fórmula que inventara, Planck supôs que, na interação dos osciladores com a radiação, ou seja, na interação da radiação com a matéria, no equilíbrio, as energias possíveis eram da forma
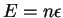
, com
sendo
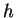
um parâmetro a determinar experimentalmente. Neste caso o cálculo do valor médio dá:
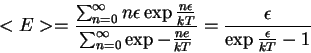
= \frac{\sum_{n=0}^{\infty}n\epsilon\exp{\-\frac{n\epsil... ...frac{ne}{kT}}} = \frac{\epsilon}{ \exp{\frac{\epsilon}{kT}}-1} \end{displaymath}" width="311" border="0" height="53">
ou
e, finalmente,
que é a fórmula de Planck. Os valores permitidos para a troca de energia foram denominados ``quanta'' de energia. Planck falou deles:``Tratou-se de uma hipótese puramente formal, e não refleti muito sobre ela, mas apenas sobre o fato de que, sob quaisquer circunstâncias, custasse o que custasse, um resultado positivo tinha de ser obtid
![]() a freqúência natural do oscilador. Posto numa região onde existe radiação em equilíbrio térmico, o oscilador executará oscilações forçadas, sendo a ``driving force'' a força elétrica que atua sobre a carga. Planck mostrou que, no equilíbrio (a dissipação considerada é a reação da radiação) estabelece-se a seguinte relação:
a freqúência natural do oscilador. Posto numa região onde existe radiação em equilíbrio térmico, o oscilador executará oscilações forçadas, sendo a ``driving force'' a força elétrica que atua sobre a carga. Planck mostrou que, no equilíbrio (a dissipação considerada é a reação da radiação) estabelece-se a seguinte relação:![]() devia ser proporcional a
devia ser proporcional a ![]() para
para ![]() pequeno, o que era inconsistente com a fórmula de Wien. Logo que as visitas saíram, Planck atacou o problema de achar uma nova fórmula empírica que satisfizesse a nova exigência, e obteve, já numa notação que ele introduziria dois meses depois6
pequeno, o que era inconsistente com a fórmula de Wien. Logo que as visitas saíram, Planck atacou o problema de achar uma nova fórmula empírica que satisfizesse a nova exigência, e obteve, já numa notação que ele introduziria dois meses depois6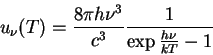
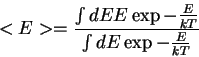 = \frac{\int dE E \exp{-\frac{E}{kT}}}{\int dE \exp{-\frac{E}{kT}}} \end{displaymath}" width="199" border="0" height="57">
= \frac{\int dE E \exp{-\frac{E}{kT}}}{\int dE \exp{-\frac{E}{kT}}} \end{displaymath}" width="199" border="0" height="57"> 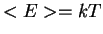 =kT$" width="103" align="middle" border="0" height="34">, e a fórmula (incorreta) de Rayleigh. De maneira inteiramente pragmática, para obter a fórmula que inventara, Planck supôs que, na interação dos osciladores com a radiação, ou seja, na interação da radiação com a matéria, no equilíbrio, as energias possíveis eram da forma
=kT$" width="103" align="middle" border="0" height="34">, e a fórmula (incorreta) de Rayleigh. De maneira inteiramente pragmática, para obter a fórmula que inventara, Planck supôs que, na interação dos osciladores com a radiação, ou seja, na interação da radiação com a matéria, no equilíbrio, as energias possíveis eram da forma 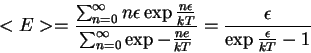 = \frac{\sum_{n=0}^{\infty}n\epsilon\exp{\-\frac{n\epsil... ...frac{ne}{kT}}} = \frac{\epsilon}{ \exp{\frac{\epsilon}{kT}}-1} \end{displaymath}" width="311" border="0" height="53">
= \frac{\sum_{n=0}^{\infty}n\epsilon\exp{\-\frac{n\epsil... ...frac{ne}{kT}}} = \frac{\epsilon}{ \exp{\frac{\epsilon}{kT}}-1} \end{displaymath}" width="311" border="0" height="53"> 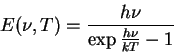
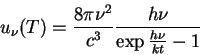
Nenhum comentário:
Postar um comentário